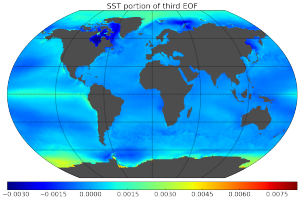
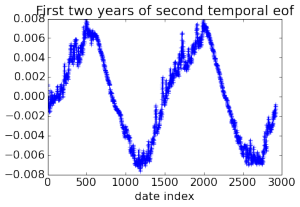
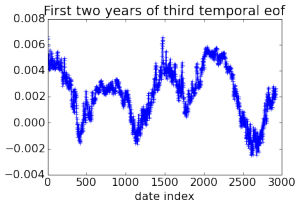
Here are some pretty pictures of empirical orthogonal functions (principal components in climatology jargon) calculated for the 3D field of ocean temperatures using data collected over 32 years, generated by computing a rank 20 PCA of a 2 Tb matrix.
I’ve been doing a lot of programming recently, implementing truncated SVDs in Spark on large datasets (hence the pictures above). I’m new to this game, but I suspect that Spark should only be used for linear algebra if you really need linear algebra as part of your larger Spark workflow: in my experience, you have to fiddle with too many esoteric knobs (e.g., several different memory settings, several network timeout settings, using the correct type of serialization at the correct location within your code) that are dependent on the size and nature of your data to make Spark run without strange errors, much less run efficiently. Then there’s the annoying JVM array size restriction: arrays are indexed by 4-bit integers, so can have at most 2^31-1 (about 2.147 billion) entries in an array. Thus a matrix with 6 million rows can only have about 360 columns, and the largest square array you can form is about 46K squared. Another way to look at this is that an array of Java floats can hold at most about 8.5 Gb. Compare this with C/C++ where your array size is essentially limited only by the amount of memory on your machine.
If *all* you’re doing is linear algebra, I recommend using a purpose-built tool, like Skylark (which we’re working on making callable from Spark). Possibly the only serious advantage Spark has over MPI-based solutions is that it can theoretically work with an unlimited amount of data, since it doesn’t need to store it all in RAM. You just have to be very careful how you process it, due to the aforementioned JVM array size restrictions.